TopCoder Open 2017 final round is today at 19:30 CEST. Tune in at https://youtu.be/qrlDoP3JQkI to hear me, pashka and Endagorion discuss! This time we should have problem statements at the beginning of the round :)
Tuesday, October 24, 2017
Monday, October 23, 2017
Commentary stream for TopCoder Open 2017 Semifinal 2 with Egor
We'll try to do live commentary of TopCoder Open 2017 Semifinal 2 with Egor on https://youtu.be/AqpjM86iZlc - tune in at 19:30 CEST!
Sunday, October 8, 2017
A randomized week
The Aug 14 - Aug 20 week contained the usual suspects: a TopCoder SRM and a Codeforces round. First off, TopCoder SRM 719 took place in the early Tuesday hours (problems, results, top 5 on the left, analysis). yanQval was a lot faster than everybody else and won the round - well done!
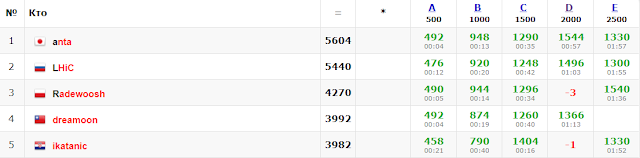
Codeforces Round 429 followed on Friday (problems, results, top 5 on the left, analysis). anta and LHiC have both solved their final fifth problem with only a few minutes to spare and thus obtained quite a margin at the top of the scoreboard - way to go!
Problem D in this round allowed for a cute randomized solution that in my view is a bit easier than the one from the official analysis. The problem was: you are given an array of 300000 numbers, and 300000 queries of the following form: a segment [l;r] and a number k, for which you need to find the smallest number that appears on at least 1/k of all positions in the given segment of the array. Note that k is at most 5, so the number must be quite frequent within the segment. Can you see how to use that fact to implement a simple randomized solution?
And finally, I've checked out CodeChef August 2017 Cook-Off on Sunday (problems, results, top 5 on the left, my screencast). EgorK was at the top of the standings with 4 problems for quite some time, but gennady.korotkevich has then submitted his fourth and fifth problems in rapid succession and won the competition. Congratulations!
In my previous summary, I have mentioned a problem that I have set for Google Code Jam 2017 finals: you are given a number k between 3 and 10000. Output any simple undirected graph with at most 22 vertices that has exactly k spanning trees.
The approach that works the most frequently in such problems is to learn several transitions that help cover all required numbers. For example, if we could come up with a way to transition from a graph with k spanning trees to graphs with 2k and 2k+1 spanning trees by adding one vertex, the problem would be solved. Alas, this does not seem possible, as it's not clear how to achieve that extra "+1" spanning tree.
As explicit construction turns out to be hard to impossible, we have to turn to more experimental approaches. One thing that stands out is that there's an enormous amount of graphs on 22 vertices, and while they have at most 2220 spanning trees, many have under 10000 spanning trees, and thus we can hope that for each k in the given range there are many possible answers. So the next idea is to try generating random graphs and checking how many spanning trees those graphs have using the matrix tree theorem, hoping to find all numbers between 3 and 10000 at least once.
It turns out that some amounts of trees are more difficult to achieve than others, so this approach by itself is not sufficient to generate all answers within reasonable time. However, there are numerous different ideas that help it find all required numbers faster, and thus help get the problem accepted. I won't be surprised if everybody who got this problem accepted at the Code Jam has used a different approach :) My experimentation led me down the following path:
Codeforces Round 429 followed on Friday (problems, results, top 5 on the left, analysis). anta and LHiC have both solved their final fifth problem with only a few minutes to spare and thus obtained quite a margin at the top of the scoreboard - way to go!
Problem D in this round allowed for a cute randomized solution that in my view is a bit easier than the one from the official analysis. The problem was: you are given an array of 300000 numbers, and 300000 queries of the following form: a segment [l;r] and a number k, for which you need to find the smallest number that appears on at least 1/k of all positions in the given segment of the array. Note that k is at most 5, so the number must be quite frequent within the segment. Can you see how to use that fact to implement a simple randomized solution?
And finally, I've checked out CodeChef August 2017 Cook-Off on Sunday (problems, results, top 5 on the left, my screencast). EgorK was at the top of the standings with 4 problems for quite some time, but gennady.korotkevich has then submitted his fourth and fifth problems in rapid succession and won the competition. Congratulations!
In my previous summary, I have mentioned a problem that I have set for Google Code Jam 2017 finals: you are given a number k between 3 and 10000. Output any simple undirected graph with at most 22 vertices that has exactly k spanning trees.
The approach that works the most frequently in such problems is to learn several transitions that help cover all required numbers. For example, if we could come up with a way to transition from a graph with k spanning trees to graphs with 2k and 2k+1 spanning trees by adding one vertex, the problem would be solved. Alas, this does not seem possible, as it's not clear how to achieve that extra "+1" spanning tree.
As explicit construction turns out to be hard to impossible, we have to turn to more experimental approaches. One thing that stands out is that there's an enormous amount of graphs on 22 vertices, and while they have at most 2220 spanning trees, many have under 10000 spanning trees, and thus we can hope that for each k in the given range there are many possible answers. So the next idea is to try generating random graphs and checking how many spanning trees those graphs have using the matrix tree theorem, hoping to find all numbers between 3 and 10000 at least once.
It turns out that some amounts of trees are more difficult to achieve than others, so this approach by itself is not sufficient to generate all answers within reasonable time. However, there are numerous different ideas that help it find all required numbers faster, and thus help get the problem accepted. I won't be surprised if everybody who got this problem accepted at the Code Jam has used a different approach :) My experimentation led me down the following path:
- Since some numbers are hard to get, we try to steer the random graphs towards those numbers. Suppose we have a "goal" number we're trying to achieve. The easiest way to do that is to avoid recreating the graph from scratch, but instead take the graph from the previous attempt, and check if it has less trees than the goal, or more. In the former case, we add a random edge to it, and otherwise remove one. As a result, we're more likely to hit the goal, and as soon as we do it, we pick another goal from the yet unseen numbers and repeat the process.
- This process has an unfortunate bad state: when we remove an edge, we can make the graph disconnected, thus having 0 spanning trees. At this point we start adding random edges, but if the graph stays disconnected, it keeps having 0 spanning trees. Finally, we add an edge that connects the graph back, but since we have added so many other edges in the meantime, suddenly the graph has a lot of spanning trees, way more than we need. So we need to remove a lot of edges to get back to reasonable numbers, and may well jump back to 0 in the process. Having noticed this happening, I've modified the process to never remove an edge that would make the graph disconnected.
- Finally, we get almost all numbers we need! After a minute or so, my solution has generated all numbers between 3 and 10000 except 13 and 22 (if I remember correctly). The final idea is that small numbers can still be generated by an explicit construction: a cycle with k vertices has k spanning trees. Since we're allowed at most 22 vertices, 13 and 22 can be done using a cycle.
That's all for my solution, but I have one more question for you: why is 22 so hard to get? In particular, does there exist a simple undirected graph with at most 21 vertices that has 22 spanning trees? I strongly suspect that the answer is no, but don't know for sure.
Thanks for reading, and check back later!
Subscribe to:
Posts (Atom)