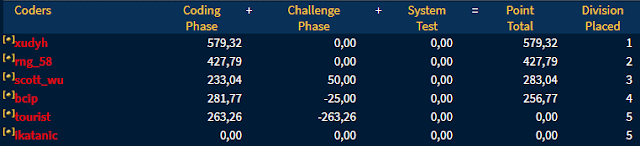
The Sep 18 - Sep 24 week featured the second Open Cup stage: the Grand Prix of Ural (
problems,
results, top 5 on the left). The Seoul National U 2 team continued to amaze, this time claiming the victory by 1 problem to Past Glory and by 2 problems to everybody else. Very well done!
Later on Sunday, Codeforces hosted a contest titled "Manthan, Codefest 17" (
problems,
results, top 5 on the left,
analysis). anta has stumbled on the tricky problem D (less than a third of contestants who submitted got it accepted), but has still came out clearly on top thanks to being the only contestant to submit all problems. Congratulations on the victory!
In
my previous summary, I have mentioned a couple of problems. One was with a recursive background: there are many contestants taking part in a competition, and top
c will be awarded with t-shirts. There are
n available t-shirt sizes (
n<=200000). Each contestant has indicated one of two things: either they need a t-shirt with some concrete size, or they need a t-shirt with one of the two concrete adjacent sizes. More precisely, for each size
i we know the number
ai of contestants (up to 10
8) that need a t-shirt of size
i, and the number
bi of contestants (also up to 10
8) that need either a t-shirt of size
i or a t-shirt of size
i+1. What is the minimal number of t-shirts we need to buy in order to be able to give t-shirts to top
c contestants, no matter which ones end up in top
c?
First, we can notice that we need to buy such set of t-shirts that in the resulting (huge) graph there's a full matching for any set of
c nodes in the left part.
Hall's theorem gives us an equivalent formulation: we need to make sure that for any set of sizes for which we buy
x t-shirts in total, and
x is less than
c, the number of people who can only wear a t-shirt from this set must not exceed
x.
Then, we can notice that we can only consider segments of sizes, and not arbitrary sets, in the above condition, as when we have multiple disjoint segments that violate the constraint together, one of them will also provide a constraint violation.
Then, just like in many other problems with constraints on segments, we can buy the t-shirts greedily: going in increasing order of sizes, for each size, we will buy just enough t-shirts to make sure the constraint is not violated for all segments that ends with this size. It doesn't make sense to buy more of this size as we can replace those extra t-shirts with ones of size one higher without making things worse.
Formally speaking,
si=max(min(
c,
ai), min(
c,
ai+
bi-1+
ai-1)-
si-1, min(
c,
ai+
bi-1+
ai-1+
bi-2+
ai-2)-
si-2-
si-1, ...). As we move from
i to
i+1, the arguments to max() change in the following way: the subtracted part increases by
si for all terms, the
a+
b part increases by
ai+1+
bi, and we get a new term. The latter causes some terms to jump over
c, in which case the corresponding min() will forever stay equal to
c, and these terms will be zero or negative in all subsequent steps, so we can forget about them.
This leads to the following approach: let's keep a set of terms for which the min() is still less than
c, then we only need to be able to add a constant to the positive part of all terms, add a constant to the negative part of all terms, to find all terms where the positive part exceeds
c, and to find the term with the largest difference between positive and negative parts. Such set of operations can be most straightforwardly implemented by keeping two priority queues of those terms: ordered by positive part and ordered by difference, and to implement adding a constant by keeping an extra "global shift" variable.
This yields a O(
nlogn) solution which is fast enough, but it can also be made O(
n) as described in
the official analysis.
Another problem I mentioned was: two players have a sequence of 50000 integers, and alternately take numbers from either end of the sequence. When all numbers have been taken, each player computes the bitwise xor of their numbers, and the one with a higher bitwise xor wins. Who will win?
I have described our solution in
this comment, but I still feel a bit uneasy about it. It can probably be proven by induction, but it would seem that in such simple setting there should be a simple argument that proves it. I'm really curious to see such argument, please share if you know one!
Finally, I've just remembered an interesting bit about the TopCoder problem which I explained in
the previous summary, about the attractions, mornings, evenings and constraints. During the contest, I was unable to come up with a max flow solution even though I felt like one is possible, and out of desperation started to implement backtracking that greedily does things that are obviously good to do, branches when we don't have an obvious next step, and cuts branches that are definitely worse than the current best answer. To my surprise, I've received a wrong answer instead of time limit exceeded on the system test. The reason for that was that I assumed that I've taken a transitive closure of the set of constraints when implementing the solution, and forgot to actually take the closure. After making this fix, the backtracking passed the system test in the practice room in 42ms :)
Thanks for reading, and check back later for more September stories!